참고자료: 밑바닥부터 시작하는 딥러닝

1. 간단한 구현부터
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1 * w1 + x2 * w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1👉🏻앞선 논리회로를 파이썬으로 구현하면 다음과 같다.
2. 가중치와 편향 도입
이전에 구현한 코드를 수정해보자!
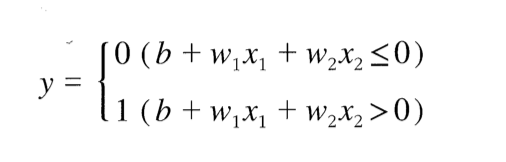
👉🏻여기서 b는 편향이다.
import numpy as np
x = np.array([0, 1])
w = np.array([0.5, 0.5])
b = -0.7
print(np.sum(w * x) + b)
#-0.19999999999999996
3. 가중치와 편향 구현하기
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1👉🏻가중치와 편향을 도입한 AND 게이트이다.
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5]) #AND와는 가중치 (w와 b)만 다르다!
b = 0.7
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2 #AND와는 b만 다르다!
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1👉🏻NAND와 OR 게이트이다. 모두 같은 구조의 퍼셉트론이다.
'그 땐 AI했지 > 그 땐 DeepLearning했지' 카테고리의 다른 글
| [TAVE/밑딥] ch02 퍼셉트론 | 05 다층 퍼셉트론이 충돌한다면 (0) | 2022.05.27 |
|---|---|
| [TAVE/밑딥] ch02 퍼셉트론 | 04 퍼셉트론의 한계 (0) | 2022.05.27 |
| [TAVE/밑딥] ch02 퍼셉트론 | 02 단순한 논리 회로 (0) | 2022.05.26 |
| [TAVE/밑딥] ch02 퍼셉트론 | 01 퍼셉트론이란? (0) | 2022.05.26 |
| [TAVE/PyTorch] ch03 선형 회귀 | 07 커스텀 데이터셋 (0) | 2022.04.28 |



