728x90
참고자료: 밑바닥부터 시작하는 딥러닝


1. 표기법 설명

👉🏻표기법은 다음과 같다. 하나씩 살펴보자!
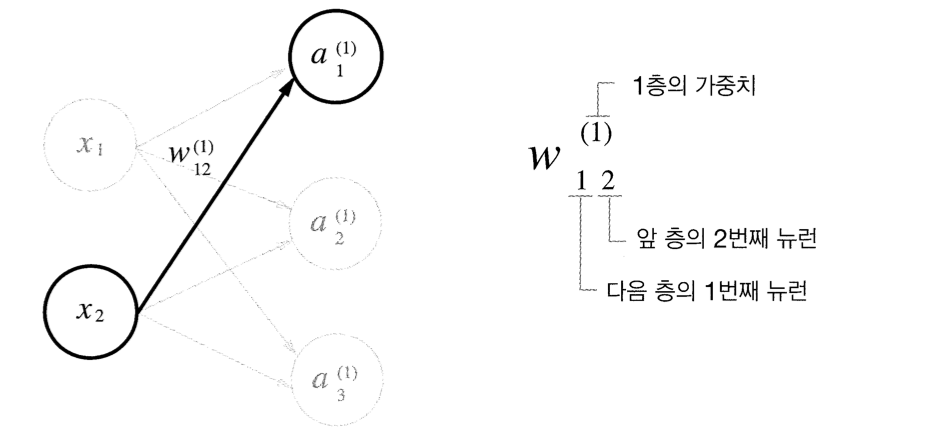
👉🏻가중치와 은닉층 뉴런의 오른쪽 위에 '(1)'이 붙어있다. 이는 1층의 가중치, 1층의 뉴런임을 뜻하는 번호이다.
👉🏻가중치의 오른쪽 아래 두 숫자는 차례로 다음 층 뉴런의 인덱스와 앞 층 뉴런의 인덱스 번호이다.
2. 각 층의 신호 전달 구현하기
1층으로 가는 과정을 구현해보자

👉🏻편향(b)을 뜻하는 뉴런이 추가 되었다. 편향 뉴런은 하나이기 때문에 오른쪽 아래 인덱스가 하나밖에 없다.

👉🏻수식은 다음과 같다. a1(첫 은닉층의 첫 뉴런) = x1 * 가중치 + x2 * 가중치 + 편향

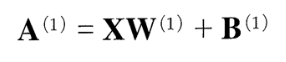
👉🏻행렬의 곱을 이용해 가중치 부분을 간소화했다. 이를 넘파이의 다차원 배열을 이용해 구현하면 다음과 같다.
import numpy as np
X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
print(W1.shape) #(2, 3)
print(X.shape) #(2,)
print(B1.shape) #(3,)
A1 = np.dot(X, W1) + B1👉🏻X는 원소가 2개인 1차원 배열, W1은 2*3 행렬!
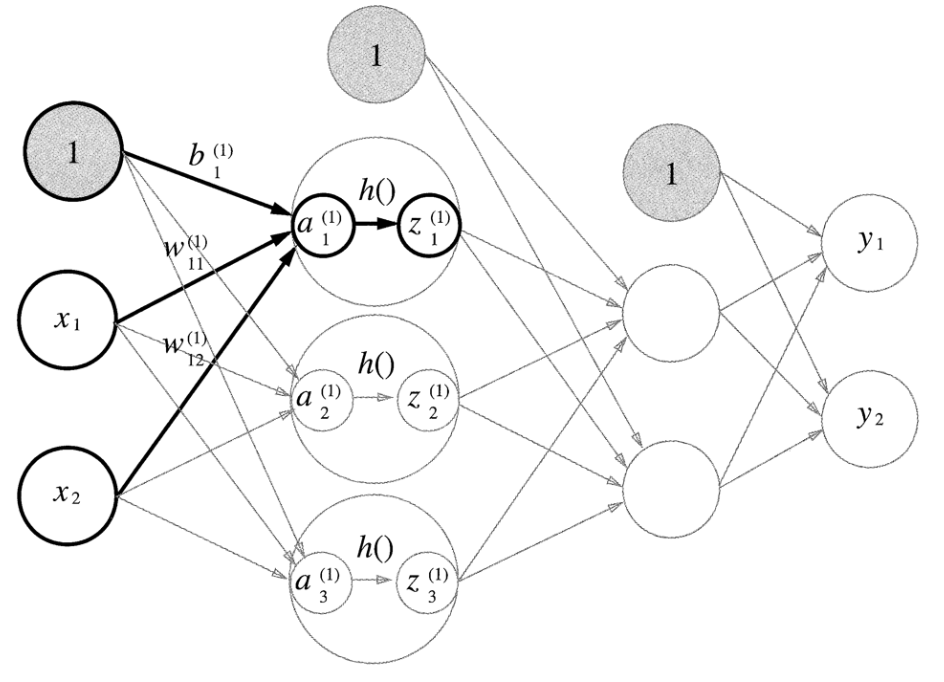
👉🏻그림으로 표현하면 다음과 같다. 은닉층에서의 가중치 합(가중 신호와 편향의 총합)을 a로 표기하고 활성화 함수 h()로 변환된 신호를 z로 표기한다. 여기서 활성화 함수는 시그모이드 함수를 사용한다고 하고 파이썬을 구현하면 다음과 같다.
import numpy as np
X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
A1 = np.dot(X, W1) + B1
def sigmoid(x):
return 1 / (1 + np.exp(-x))
Z1 = sigmoid(A1)
print(A1) #[0.3 0.7 1.1]
print(Z1) #[0.57444252 0.66818777 0.75026011]👉🏻짠! 이렇게 1층으로 가는 과정을 구현해 보았다!
1층에서 2층으로 가는 과정을 구현해보자

W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
print(Z1.shape) #(3,)
print(W2.shape) #(3, 2)
print(B2.shape) #(2,)
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)
print(Z2) #[0.62624937 0.7710107 ]
2층에서 출력층으로 가는 과정을 구현해보자!

def identify_function(x):
return x
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, W3) + B3
Y = identify_function(A3)👉🏻항등 함수 identify_function을 정의해서 이용했다.
👉🏻그림을 보면 출력층의 활성화 함수를 º(시그마)로 표시했다.
3. 구현 정리
import numpy as np
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def identify_function(x):
return x
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identify_function(a3)
return Y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) #[0.31682708 0.69627909]👉🏻현재까지 내용을 정리해보았다!
- init_network 함수: 가중치와 편향을 초기화하고 이들을 network 딕셔너리에 저장한다.
- forward 함수: 입력 신호를 출력으로 변환하는 처리 과정을 구현하고 있다.
728x90
'그 땐 AI했지 > 그 땐 DeepLearning했지' 카테고리의 다른 글
| [TAVE/밑딥] ch03 신경망 | 03 다차원 배열의 계산 (0) | 2022.06.03 |
|---|---|
| [TAVE/밑딥] ch03 신경망 | 02 활성화 함수 (0) | 2022.06.02 |
| [TAVE/밑딥] ch03 신경망 | 01 퍼셉트론에서 신경망으로 (0) | 2022.06.02 |
| [TAVE/밑딥] ch02 퍼셉트론 | 06 NAND에서 컴퓨터까지 (0) | 2022.05.27 |
| [TAVE/밑딥] ch02 퍼셉트론 | 05 다층 퍼셉트론이 충돌한다면 (0) | 2022.05.27 |



