참고자료: 이것이 코딩테스트다

그래프
📌노드와 노드 사이에 연결된 간선의 정보를 가지고 있는 자료구조
👉🏻그래프 구현 방식
- 인접 행렬: 2차원 배열을 사용하는 방식
- 인접 리스트: 리스트를 사용하는 방식
🐰다양한 그래프 알고리즘을 알아보자!
1️⃣ 서로소 집합
📌공통 원소가 없는 두 집합
✅서로소 집합 자료구조
📌서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조를 말한다.
👉🏻union(합집합)연산과 find(찾기)연산으로 조작할 수 있어 union-find 자료구조로 불리기도 한다.
👉🏻트리 자료구조를 이용해 집합을 표현하고 계산 알고리즘은 다음과 같다.
- union(합집합) 연산을 확인하여, 서로 연결된 두 노드 A, B를 확인한다.
- A와 B의 루트 노드 A', B'를 각각 찾는다.
- A', B'의 부모 노드로 설정한다(B'가 A'를 가리키도록 한다).
- 모든 union(합집합) 연산을 처리할 때까지 1번 과정을 반복한다.
👉🏻전체 집합과 union 연산이 다음과 같은 상황을 생각해보자.
- 전체 집합: {1, 2, 3 , 4, 5, 6}
- union 연산: union 1, 4, union 2, 3, union 2, 4, union 5, 6
👉🏻6개의 노드와 4개의 간선의 그래프로 바꾸어 생각할 수 있다. 트리 구조 상 번호가 작은 노드가 부모가 되고 번호가 큰 노드가 자식이 된다.

👉🏻해당 그림은 {1, 2, 3, 4}와 {5, 6}이라는 두 집합으로 나눌 수 있다. 이렇게 union 연산을 토대로 그래프를 그리면 '연결성'으로 손쉽게 집합의 형태를 확인할 수 있다.

👉🏻초기 단계에 모든 원소가 자기 자신을 부모로 가지도록 초기화한다. 실제 루트를 확인하고자 할 떄는 재귀적으로 부모를 거슬러 올라가서 최종적인 루트 노드를 찾아야 한다.

👉🏻첫 번째 연산 union 1, 4를 확인하면, 1과 4를 합친다. 이 때는 노드 1과 노드 4의 루트 노드를 각각 찾는다. 현재 루트 노드는 각각 1과 4이기 때문에 더 큰 번호에 해당하는 루트 노드 4의 부모를 1로 설정한다.

👉🏻union 2, 3을 확인하면 2와 3을 합친다.

👉🏻union 2, 4

👉🏻union 5, 6
👉🏻해당 알고리즘은 union 연산을 효과적으로 수행하기 위해 '부모 테이블'을 항상 가지고 있어야 한다. 또한 루트 노드를 즉시 계산할 수 없고, 부모 테이블을 계속해서 확인하며 거슬러 올라가야 한다. 예를 들어 위의 노드 3을 살펴보자면 부모 노드는 2이고 루트 노드는 1이다. 다시 말해 서로소 집합 알고리즘으로 루트를 찾기 위해서 재귀적으로 부모를 거슬러 올라가야 한다.
#특정 원소가 속한 집합 찾기
def find_parent(parent, x):
#루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
return find_parent(parent, parent[x])
return x
#두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
#노드의 개수와 간선(union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1) #부모 테이블 초기화
#부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
#union 연산을 각각 수행
for i in range(e):
a, b = map(int, input().split())
union_parent(parent, a, b)
#각 원소가 속한 집합 출력
print('각 원소가 속한 집합: ', end = '')
for i in range(1, v + 1):
print(find_parent(parent, i), end = ' ')
print()
#부모 테이블 내용 출력
print('부모 테이블: ', end = '')
for i in range(1, v + 1):
print(parent[i], end = ' ')
#각 원소가 속한 집합: 1 1 1 1 5 5
#부모 테이블: 1 1 2 1 5 5👉🏻소스코드는 다음과 같다. 하지만 해당 소스코드는 find 함수가 비효율적으로 동작한다. 아래 예시를 살펴보자.

👉🏻노드 5의 루트 노드를 알아내기 위해 '노드 5 → 노드 4 → 노드 3 → 노드 2 → 노드 1' 순서대로 부모 노드를 거슬러 올라가야 하므로 최대 O(V)의 시간이 소요된다. 결과적으로 노드의 개수가 V개이고 union 연산의 개수가 M개일 때 전체 시간 복잡도는 O(VM)이 되어 비효율적이다.
🐰이러한 find 함수를 경로 압축 기법을 사용하면 최적화가 가능하다.
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]👉🏻find_parent 함수를 다음과 같이 수정해준다. find 함수를 재귀적으로 호출한 뒤에 부모 테이블값을 갱신한다. 그러면 해당 노드의 루트 노드가 바로 부모 노드가 된다.

✅서로소 집합 알고리즘의 시간 복잡도
👉🏻경로 압축 방법을 사용하면 노드의 개수가 V개이고 최대 V - 1개의 union 연산과 M개의 find 연산이 가능할 때 \(O(V + M(1 + log_{2-M/V}V))\)이다.
✅서로소 집합을 활용한 사이클 판별
👉🏻서로소 집합은 무방향 그래프 내에서의 사이클을 판별할 때 사용할 수 있다.
- 각 간선을 확인하며 두 노드의 루트 노드를 확인한다.
- 루트 노드가 서로 다르다면 두 노드에 대하여 union 연산을 수행한다.
- 루트 노드가 서로 같다면 사이클(Cycle)이 발생한 것이다.
- 그래프에 포함되어 있는 모든 간선에 대하여 1번 과정을 반복한다.
👉🏻간선을 (1, 2) → (1, 3) → (2, 3) 순서로 확인하며 부모 노드를 변경해준다.
#특정 원소가 속한 집합 찾기
def find_parent(parent, x):
#루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
#두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
#노드의 개수와 간선(union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1) #부모 테이블 초기화
#부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
cycle = False #사이클 발생 여부
for i in range(e):
a, b = map(int, input().split())
#사이클이 발생한 경우 종료
if find_parent(parent, a) == find_parent(parent, b):
cycle = True
break
#사이클이 발생하지 않았다면 합집합(union) 수행
else:
union_parent(parent, a, b)
if cycle:
print("사이클이 발생했습니다.")
else:
print("사이클이 발생하지 않았습니다.")
2️⃣신장 트리
📌하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프

👉🏻오른쪽이 가능한 신장 트리 예시이다.

👉🏻위 두 개는 신장 트리가 아닌 부분 그래프 예시이다.
✅크루스칼 알고리즘
📌최소 신장 트리 알고리즘: 최소한의 비용으로 신장트리를 찾는 알고리즘. 대표적으로 크루스칼 알고리즘이 있다.
👉🏻크루스칼 알고리즘은 그리디 알고리즘으로 분류된다. 간선에 대하여 정렬을 수행한 뒤에 가장 거리가 짧은 간선부터 집합에 포함시킨다. 이때 사이클을 발생시킬 수 있는 간선의 경우 집합에 포함시키지 않는다.
- 간선 데이터를 비용에 따라 오름차순으로 정렬한다.
- 간선을 하나씩 확인하여 현재의 간선이 사이클을 발생시키는지 확인한다.
- 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킨다.
- 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않는다.
- 모든 간선에 대하여 2번을 반복한다.

왼쪽 그래프의 최소 신장 트리가 오른쪽 그림이라는 것을 구해보자!
👉🏻최소 신장 트리는 일종의 트리 자료구조이므로 신장 트리에 포함되는 간선의 개수는 '노드의 개수 - 1'이다.
🐰최소 신장 트리 알고리즘 한 눈에 보기
0️⃣step 0

👉🏻그래프의 모든 간선 정보만 따로 빼내어 정렬을 수행한다. (원래는 간선 정보를 따로 리스트에 담아 정렬하지만 그림은 가독성을 위해 노드 데이터 순서에 따라 데이터를 나열했다.)
1️⃣step 1

👉🏻가장 짧은 노선인 (3, 4)를 선택해 union 함수를 수행한다. 노드 3과 노드 4를 동일한 집합에 속하도록 만든다.
2️⃣step 2

👉🏻다음으로 짧은 간선 (4, 7)을 선택하고 union 함수를 호출한다.
3️⃣step 3

👉🏻다음으로 짧은 간선 (4, 6)을 선택하고 union 함수를 호출한다.
4️⃣step 4

👉🏻다음으로 짧은 간선 (6, 7)을 선택한다. 노드 6과 노드 7의 루트가 이미 동일한 집합에 포함되어 있으므로 신장 트리에 포함하지 않는다.
5️⃣step 5-9





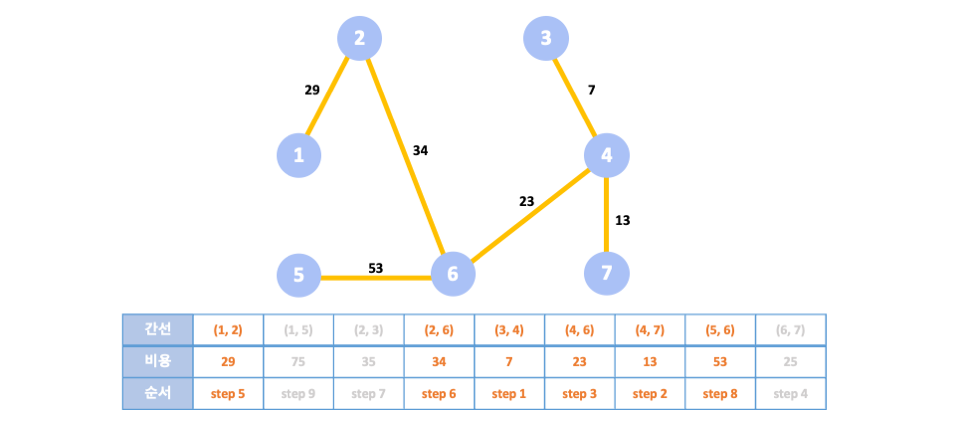
👉🏻같은 과정을 반복한다.
#특정 원소가 속한 집합 찾기
def find_parent(parent, x):
#루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
#두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
#노드의 개수와 간선(union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1) #부모 테이블 초기화
#모든 간선을 담을 리스트와 최종 비용을 담을 변수
edges = []
result = 0
#부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
#모든 간선에 대한 정보를 입력받기
for _ in range(e):
a, b, cost = map(int, input().split())
#비용순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
edges.append((cost, a, b))
#간선을 비용순으로 정렬
edges.sort()
#간선을 하나씩 확인하며
for edge in edges:
cost, a, b = edge
#사이클이 발생하지 않는 경우에만 집합에 포함
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
result += cost
print(result)👉🏻소스 코드는 다음과 같다.
✅크루스칼 알고리즘의 시간 복잡도
👉🏻간선의 개수가 E개일 때, O(ElogE)의 시간 복잡도를 가진다.
👉🏻크루스칼 알고리즘에서 시간이 가장 오래 걸리는 부분이 간선을 정렬하는 작업이며, E개의 데이터를 정렬했을 때의 시간 복잡도가 O(ElogE)이기 때문이다.
3️⃣위상 정렬
📌방향 그래프의 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것'이다. 정렬 알고리즘의 일종이다.
현실 세계에서 위상정렬 예를 들어보자면 컴퓨터공학과의 커리큘럼이 있다. 아래 그림을 보자!

👉🏻알고리즘 강의를 수강하기 위해 자료 구조 과목을 수강해야 하고 고급 알고리즘 강의를 수강하기 위해서는 자료 구조와 알고리즘 강의를 먼저 수강해야 한다. 이 때 각 과목이 노드이고 화살표가 방향을 갖는 간선으로 볼 수 있다.
📌진입차수: 특정한 노드로 들어오는 간선의 개수이다.
👉🏻위상 정렬 알고리즘은 다음과 같다.
- 진입차수가 0인 노드를 큐에 넣는다.
- 큐가 빌 때까지 다음의 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
🐰위상 정렬 한 눈에 보기
0️⃣step 0

👉🏻초기 단계에는 진입차수가 0인 노드가 1뿐이므로 큐에 노드 1을 삽입한다.
0️⃣step 1

👉🏻큐에 들은 노드 1을 꺼내 연결된 간선들을 제거한다. 그리고 다시 진입차수가 0이 된 노드(2, 5)들을 큐에 넣는다.
2️⃣step 2

👉🏻노드 2를 꺼내 연결된 간선들을 제거한다. 그리고 다시 진입차수가 0이 된 노드(3)를 큐에 넣는다.
1️⃣step 3~7

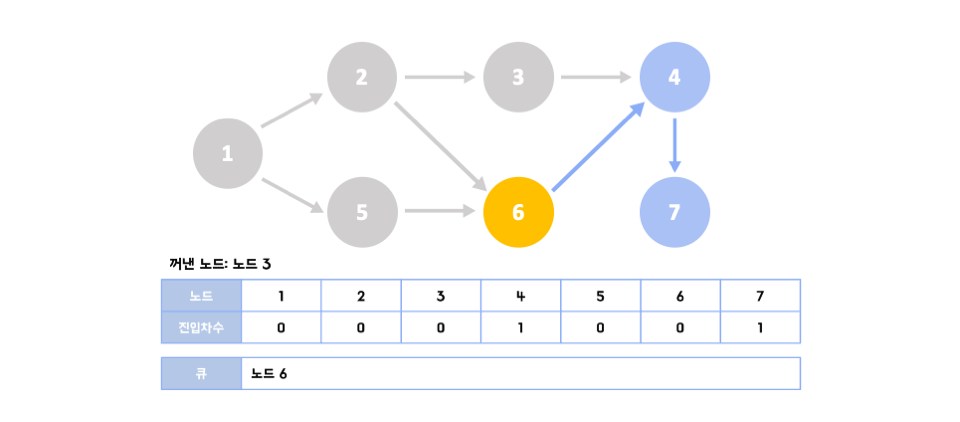

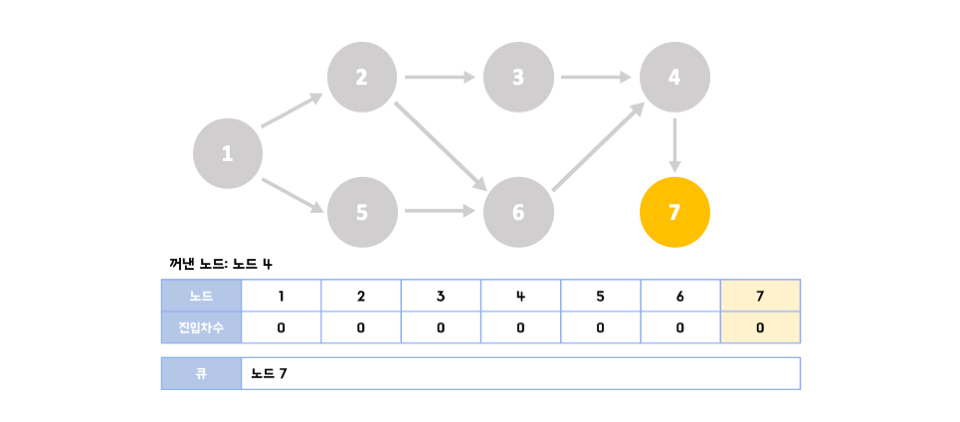
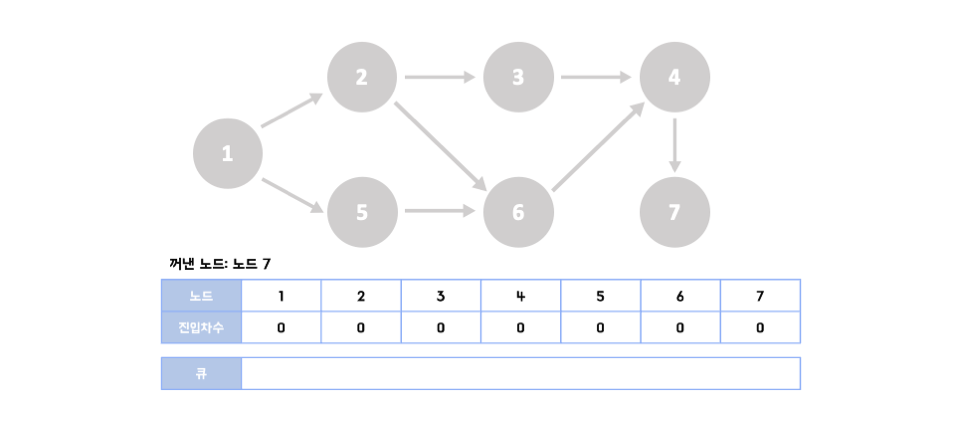
👉🏻같은 과정을 반복한다. 이 과정을 수행하는 동안 큐에서 빠져나간 노드를 순서대로 출력하면 이것이 바로 위상 정렬을 수행한 결과가 된다. 위상정렬은 답안이 여러 가지가 될 수 있는데 만약 한 단계에서 큐에 새롭게 들어가는 원소가 2개 이상인 경우가 있을 때(step 1)이다.
from collections import deque
#노드의 개수와 간선의 개수를 입력받기
v, e = map(int, input().split())
#모든 노드에 대한 진입차수는 0으로 초기화
indegree = [0] * (v + 1)
#각 노드에 연결된 간선 정보를 담기 위한 연결 리스트(그래프) 초기화
graph = [[] for i in range(v + 1)]
#뱡향 그래프의 모든 간선 정보를 입력받기
for _ in range(e):
a, b = map(int, input().split())
graph[a].append(b) #정점 A에서 B로 이동 가능
#진입차수를 1 증가
indegree[b] += 1
#위상 정렬 함수
def topology_sort():
result = [] #알고리즘 수행 결과를 담을 리스트
q = deque() #큐 기능을 위한 deque 라이브러리 사용
#처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for i in range(1, v + 1):
if indegree[i] == 0:
q.append(i)
#큐가 빌 때까지 반복
while q:
#큐에서 원소 꺼내기
now = q.popleft()
result.append(now)
#해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for i in graph[now]:
indegree[i] -= 1
#새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if indegree[i] == 0:
q.append(i)
#위상 정렬을 수행한 결과 출력
for i in result:
print(i, end=' ')
topology_sort()
#위의 예시의 그래프를 넣고 실행하면 아래와 같은 결과가 나온다.
#1 2 5 3 6 4 7👉🏻소스 코드는 다음과 같다.
✅위상 정렬의 시간 복잡도
👉🏻O(V + E)이다. 차례대로 모든 노드를 확인하면서 출발하는 간선을 차례로 제거해야 한다. 결과적으로 노드와 간선을 모두 확인하기 때문이다.
'그 땐 Algorithm했지 > 그 땐 Python했지' 카테고리의 다른 글
| [TAVE/이코테] ch10 그래프 이론 | 실전 문제 (0) | 2022.05.04 |
|---|---|
| [TAVE/이코테] ch09 최단 경로 | 실전 문제 (0) | 2022.04.20 |
| [TAVE/이코테] ch09 최단 경로 | 개념 정리 (0) | 2022.04.20 |
| [TAVE/파이썬 알고리즘 인터뷰] Ch13 | 최단 경로 문제 - 개념 정리 (0) | 2022.04.16 |
| [TAVE/파이썬 알고리즘 인터뷰] Ch11 | 해시 테이블 - 개념 정리 (0) | 2022.04.15 |



