참고자료: https://wikidocs.net/book/2788
PyTorch로 시작하는 딥 러닝 입문
이 책은 딥 러닝 프레임워크 PyTorch를 사용하여 딥 러닝에 입문하는 것을 목표로 합니다. 이 책은 2019년에 작성된 책으로 비영리적 목적으로 작성되어 출판 ...
wikidocs.net

데이터에 대한 이해
📌다중 선형 회귀: 다수의 x로부터 y를 예측한다.
| Quiz 1 (x1) | Quiz 2 (x2) | Quiz 3 (x3) | Final (y) |
| 73 | 80 | 75 | 152 |
| 93 | 88 | 93 | 185 |
| 89 | 91 | 80 | 180 |
| 96 | 98 | 100 | 196 |
| 73 | 66 | 70 | 142 |
👉🏻독립 변수 x의 개수가 3개이므로 식은 아래와 같다.
$$H(x)=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+b$$
파이토치로 구현하기
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)👉🏻필요한 도구들을 임포트하고 랜덤 시드를 고정한다.
#훈련 데이터
x1_train = torch.FloatTensor([[73], [93], [89], [96], [73]])
x2_train = torch.FloatTensor([[80], [88], [91], [98], [66]])
x3_train = torch.FloatTensor([[75], [93], [90], [100], [70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
# 가중치 w와 편향 b 초기화
w1 = torch.zeros(1, requires_grad=True)
w2 = torch.zeros(1, requires_grad=True)
w3 = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)$$H(x)=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+b$$
👉🏻위 식을 보면 x가 3개이므로 x를 3개 선언한다. 또 가중치 w도 3개 선언하고 편향 b를 선언한다.
#optimizer 설정
optimizer = optim.SGD([w1, w2, w3, b], lr = 1e-5)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
#H(x) 계산
hypothesis = x1_train * w1 + x2_train * w2 + x3_train * w3 + b
#cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
#cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
#100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} w1: {:.3f} w2: {:.3f} w3: {:.3f} b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, w1.item(), w2.item(), w3.item(), b.item(), cost.item()))👉🏻가설, 비용 함수, 옵티마이저를 선언한 후에 경사 하강법을 1,000회 반복한다.
백터와 행렬 연산으로 바꾸기
위의 코드는 x가 3개이기 때문에 3번 일일히 선언해주었다. 하지만 만약 x의 개수가 1,000개라면? 2,000개라면?
항상 일일히 x와 w를 선언해주어야 하기 때문에 비효율적이다.
👉🏻이러한 현상을 해결하기 위해 행렬 곱셈 연산(또는 벡터의 내적)을 사용한다.
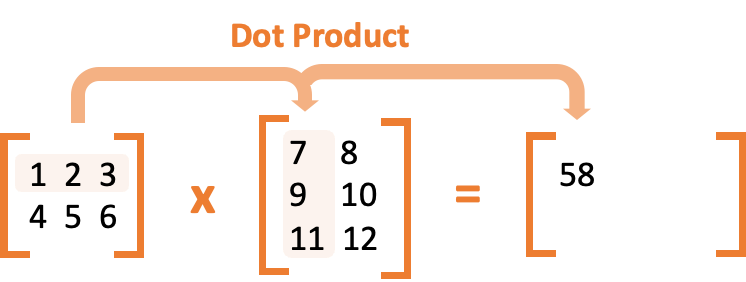
👉🏻행렬 곱셈 과정에서 벡터의 내적으로 1 x 7 + 2 x 9 + 3 x 11 = 58이 되는 과정을 보여준다. 이러한 방식으로 가설을 벡터와 행렬 연산으로 표현해보자!
백터 연산으로 이해하기
$$H(x)=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+b$$
👉🏻이 식은 아래와 같이 두 벡터의 내적으로 표현할 수 있다.
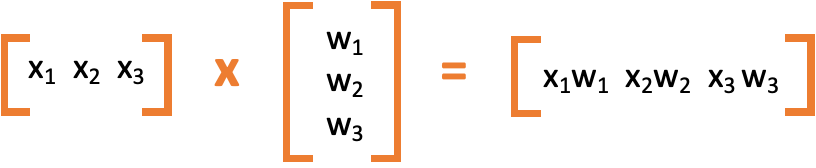
👉🏻두 벡터를 각각 X와 W로 표현하면 \(H(x) = XW\)과 같다. 이전에는 3개의 x와 3개의 w로 나타낸 반면 현재는 X와 W라는 두 개의 변수로 표현된 것을 확인할 수 있다.
행렬 연산으로 이해하기
| Quiz 1 (x1) | Quiz 2 (x2) | Quiz 3 (x3) | Final (y) |
| 73 | 80 | 75 | 152 |
| 93 | 88 | 93 | 185 |
| 89 | 91 | 80 | 180 |
| 96 | 98 | 100 | 196 |
| 73 | 66 | 70 | 142 |
📌샘플: 전체 훈련 데이터의 개수를 셀 수 있는 1개의 단위이다.
📌특성: 각 샘플에서 y를 결정하게 하는 각각의 독립 변수 x를 말한다.
👉🏻훈련 데이터는 다음과 같다. 샘플은 총 5개이고 특성은 3개이다. 그러므로 독립 변수 x는 총 15개(샘플 개수 * 특성 개수)이다.

👉🏻위의 식은 \(H(X) = XW + B\)이다. 전체적으로 훈련 데이터의 가설 연산을 3개의 변수만으로 표현해 식을 간단하게 해주며 속도의 이점을 가진다.
행렬 연산을 고려하여 파이토치로 구현하기
👉🏻먼저 훈련 데이터를 행렬로 선언한다.
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 80],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
print(x_train.shape)
print(y_train.shape)
#torch.Size([5, 3])
#torch.Size([5, 1])👉🏻x_train 하나에 모든 샘플을 선언한다. (5 x 3)행렬 X를 선언한 것과 같다.
# 가중치와 편향 선언
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)👉🏻가중치가 (3 x 1) 크기의 벡터이다. 행렬의 곱셈이 성립되려면 곱셈의 좌측에 있는 행렬(x_train)의 열의 크기와(3) 우측에 있는 행렬(w)의 행(3)의 크기가 일치해야 한다. 현재는 3으로 일치하므로 두 행렬과 벡터는 행렬곱이 가능하다.
hypothesis = x_train.matmul(W) + b👉🏻가설을 행렬곱으로 나타내면 다음과 같다. 아까와 달리 독립 변수 x를 늘리거나 줄여도 가설 선언 코드를 수정할 필요가 없다.
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 80],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
# 모델 초기화
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr = 1e-5)
np_epochs = 20
for epoch in range(nb_epochs + 1):
#H(x) 계산
#편향 b는 브로드 캐스팅되어 각 샘플에 더해집니다.
hypothesis = x_train.matmul(W) + b
#cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
#cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
print('Epoch {:4d}/{} hypothesis: {} Cost: {:.6f}'.format(
epoch, nb_epochs, hypothesis.squeeze().detach(), cost.item()
))👉🏻전체 코드는 다음과 같다. 비용 함수와 옵티마이저를 정의하고, 정해진 에포크만큼 훈련을 진행한다.
'그 땐 AI했지 > 그 땐 DeepLearning했지' 카테고리의 다른 글
| [TAVE/PyTorch] ch03 선형 회귀 | 06 미니 배치와 데이터 로드 (0) | 2022.04.28 |
|---|---|
| [Study/pytorch] ch03 선형 회귀 | 04 nn.Module로 구현하는 선형 회귀 (0) | 2022.04.21 |
| [TAVE/study] ch03 선형 회귀 | 02 자동 미분 (0) | 2022.04.07 |
| [TAVE/study] ch03 선형 회귀 | 01 선형 회귀 (0) | 2022.04.07 |
| [TAVE/study] ch02 파이토치 기초 | 04 파이썬 클래스 (0) | 2022.04.01 |



